7. 再帰¶
7.1. 再帰さん、こんにちは!¶

手続き型プログラミング言語やオブジェクト指向プログラミング言語に慣れている読者の方々には、なぜまだループが出てきてないのか疑問に思っているかもしれません。 答えは「ループってなんすか?」ですよ。実のところを言うと、関数型プログラミング言語では通常 for や while のようなループ制御を提供しません。 その代わりに、関数型プログラマは再帰と呼ばれるバカな概念に寄っかかっているのです。
導入の章で、変更できない変数がどのように説明されていたか覚えていると思います。 覚えていないなら、もっと注意深く読んでください! 再帰は数学の概念と関数を使っても説明できます。階乗のような基本的な数学的関数が再帰で表現できる良い例です。 nの階乗は1からnまでの数列の積で 1 x 2 x 3 x ... x n で表せます。あるいは n x n-1 x n-2 x ... x 1 でも表せます。 たとえば、3の階乗は 3! = 3 x 2 x 1 = 6 で、4の階乗は 4! = 4 x 3 x 2 x 1 = 24 です。 そのような関数は次のような数学的記法で表現できます。
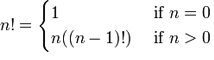
ここで分かることは、もしnが0だったら結果は1になるということです。 0より大きい数は n と n-1 の階乗の積が返ります。 n-1 の階乗は1まで展開されます:
4! = 4 x 3!
4! = 4 x 3 x 2!
4! = 4 x 3 x 2 x 1!
4! = 4 x 3 x 2 x 1 x 1
このような関数を数学的記法からErlangに翻訳したらいいんでしょうか? 変換はとても単純です。上の記法を部分部分で見てみましょう。 n!, 1 そして n((n-1)!) と if です。 ここで分かるのは関数名(n!)とガード(if)そして関数の中身(1と n((n-1)!))です。 構文の制限から n! は fac(N) に変えて、次のような結果を得られます:
-module(recursion).
-export([fac/1]).
fac(N) when N == 0 -> 1;
fac(N) when N > 0 -> N*fac(N-1).
この再帰関数はこれでおしまいです!数学的な定義とよく似てますよね、ほんとに。 パターンマッチを使って、関数定義をちょっと短く出来ます:
fac(0) -> 1;
fac(N) when N > 0 -> N*fac(N-1).
始めから再帰になっている数学の定義を変換するのは早くて簡単です。ループが出来ました! 再帰の定義を短く言えば「自分自身を呼び出している関数」です。 しかし、停止条件が必要です。(実際の呼び名は終了条件です)そうしないと、ループがずっと続いてしまいます。 私たちの例では、終了条件はnが0と等しい時です。そのときは、関数自身を呼び出さないで、再帰が止まりました。
7.2. 長さ¶
もうちょっと実用的にしてみましょう。リストの中にどれだけの要素がある数える関数を実装します。 なので最初から必要なものが分かっています:
- 終了条件
- 自分自身を呼び出す関数
- 関数を試すリスト
たいていの再帰関数では、最初に終了条件を書くのが簡単だと思います。 長さを調べるリストとして、最も単純な物はなんでしょうか?確実に空のリストがそれです。長さ0になります。 心のノートに、長さを扱うときは [] = 0 と書いておきましょう。 その次に単純なリストは長さ1のリストですね。 [_] = 1 です。 なんとなくこれで定義を書き始めてよさそうですね。こんな感じに書けます:
len([]) -> 0;
len([_]) -> 1.
すばらしい!もし長さが0か1だったら、もうリストの長さを調べられます!とっても役に立ちますね。 えっと、もちろんまだ再帰になってないので、これは役立たずですけど。で、その再帰が一番難しい部分ですが。 この関数を拡張して、自分自身を呼び出して長さが0,1よりも長いリストにも使えるようにしてみましょう。 前にも言いましたが、リストは再帰的に定義されています。このような具合です。 [1 | [2 | ... [n | []]]] これはつまり1つ以上の要素に対して [H|T] のパターンが使えるということです。 長さ1のリストは [X|[]] で定義されて、長さ2のリストは [X|[Y|[]]] とう具合です。 2番目の要素はリストであることに注意してください。これはつまり、最初の要素だけカウントして、関数は自分自身を2番目の要素に対して呼び出せばいいということです。 リストの長さがそれぞれ長さ1だとしたら、関数は次のように書きなおすことができます:
len([]) -> 0;
len([_|T]) -> 1 + len(T).
これであなたの再帰関数はリストの長さを計算するようになりました。 len/1 がどのように動作するか、分かっているリスト、たとえば [1,2,3,4] で試してみましょう:
len([1,2,3,4]) = len([1 | [2,3,4])
= 1 + len([2 | [3,4]])
= 1 + 1 + len([3 | [4]])
= 1 + 1 + 1 + len([4 | []])
= 1 + 1 + 1 + 1 + len([])
= 1 + 1 + 1 + 1 + 0
= 1 + 1 + 1 + 1
= 1 + 1 + 2
= 1 + 3
= 4
正しい答えはなんでしょうか。おめでとう!Erlangで始めて役に立つ再帰関数が書けました!

7.3. 末尾再帰の長さ¶
気づいたかもしれませんが、4つの項を持つリストの場合は、関数呼び出しを5個連鎖するまで展開していました。 これはリストが短い場合はいいですが、数百万の長さのリストの場合は問題があるでしょう。 これは無駄で、もっといい方法があります。末尾再帰をやってみましょう。
末尾再帰は上に書いた線形の処理(要素が増えれば増えるほど大きくなる処理)を逐次的な処理(全然大きくならない処理)に変更します。 関数の呼び出し方を末尾再帰にするには、それを「ひとつだけ」にすることです。 説明しましょう。先程の再帰関数を大きくさせてしまっているのは、最初の結果が2番目の結果に依存してしまっているという点です。 1 + len(Rest) は len(Rest) の答えを必要とします。関数 len(Rest) 自身は他の関数の結果を必要としています。 追加されたものは最後の一つが見つかるまでスタックされ、最後の一つが見つかったときに最終結果が計算されます。 末尾再帰はこういった演算のスタックをなくすことを狙いとしています。
これを達成するためには、関数にパラメータとして追加の一時変数を持つ必要があります。 この概念を階乗の関数を使って説明します。今回は末尾再帰になるようにします。 前述したとおり、一時変数は時々アキュムレータと呼ばれ、計算結果を保存する場所として使います;
tail_fac(N) -> tail_fac(N,1).
tail_fac(0,Acc) -> Acc;
tail_fac(N,Acc) when N > 0 -> tail_fac(N-1,N*Acc).
ここで、 tail_fac/1 と tail_fac/2 の2つを定義しました。この理由はErlangが関数にデフォルト引数を認めていないからです。(アリティが異なる場合、関数は異なります)なので、手でこれをしなければいけません。 この場合は tail_fac/1 は末尾再帰の tail_fac/2 関数を抽出したもののように振る舞います。 tail_fac/2 の隠れたアキュムレータの詳細についてはもう興味はありません。 なのでモジュールからは tail_fac/1 だけど公開します。この関数を実行するときは、このように展開します:
tail_fac(4) = tail_fac(4,1)
tail_fac(4,1) = tail_fac(4-1, 4*1)
tail_fac(3,4) = tail_fac(3-1, 3*4)
tail_fac(2,12) = tail_fac(2-1, 2*12)
tail_fac(1,24) = tail_fac(1-1, 1*24)
tail_fac(0,24) = 24
違いはなんでしょうか?いまは2つ以上の項をメモリに持つ必要がありません。 メモリ使用量は一定です。4の階乗でも100万の階乗でも同じスペースしか使いません。 ( 4! が 1M! よりもその定義として小さい数字だということを忘れてしまっていても、それだけのことです)
末尾再帰の階乗の例が身についたところで、このパターンが len/1 関数にどのように適用できるか分かるはずです。 必要なのは再帰呼び出しを「ひとつだけ」にすることです。 もし見た目で分かる例がほしければ、 +1 の部分をパラメータを追加することで関数呼び出しの中に追加することを考えるだけで結構です:
len([]) -> 0;
len([_|T]) -> 1 + len(T).
becomes:
tail_len(L) -> tail_len(L,0).
tail_len([], Acc) -> Acc;
tail_len([_|T], Acc) -> tail_len(T,Acc+1).
これで、length関数は末尾再帰になりました。
7.4. さらに末尾関数¶
もうちょっと慣れるために、あと2、3個再帰関数を書いてみましょうか。 結局、再帰関数というのはErlangに存在するループ構造(リスト内包を除く)であり、最も理解しなければいけない概念の一つなのです。 あとで他の関数型プログラミング言語を試してみる場合にも役立つので、メモをとっておきましょう!
最初に書く関数は duplicate/2 です。この関数は整数を最初のパラメータとして受け取り、なんらかの項を2番目のパラメータとして受け取ります。 それから2番目の項を1番目の整数の数だけコピーしたリストを作ります。 前のように、終了条件をまず最初に考えるとどう進めたらいいかわかります。 duplicate/2 の場合は、何かを0回繰り返すというのが最も基本的な状況です。 この場合、2番目がどんな項でも空のリストを返せばいいですね。 他の場合は関数自身を呼び出して、終了条件まで繰り返さなければなりません。 また、負の整数も -n 回などと複製することはできないので禁止しなければなりません。
duplicate(0,_) ->
[];
duplicate(N,Term) when N > 0 ->
[Term|duplicate(N-1,Term)].
一度、基本的な再帰関数が書けたら、それを末尾再帰にするのは簡単です。 リストの作成部分を一時変数に入れればいいのです。
tail_duplicate(N,Term) ->
tail_duplicate(N,Term,[]).
tail_duplicate(0,_,List) ->
List;
tail_duplicate(N,Term,List) when N > 0 ->
tail_duplicate(N-1, Term, [Term|List]).
できました!ここで対象の関数をもうちょっと変更して、末尾再帰とwhileループの両方で書いてみたいと思います。 tail_duplicate/2 関数はwhileループに使う部分を持っています。 もしErlangに似た構文を持った関数型言語でwhileループがあったら、先程の関数はこのようになります:
function(N, Term) ->
while N > 0 ->
List = [Term|List],
N = N-1
end,
List.
ここに書いたすべての要素が架空の言語でのwhileループ内にも、Erlangでの末尾再帰内にもあることに注目してください。 ただ書いてある場所だけが変わっただけです。これは適切な末尾再帰関数はwhileループのような逐次処理と似ているということを教えてくれます。
reverse/1 関数を書いて、再帰関数と末尾再帰関数を比較してみると面白い特性を「見つける」ことが出来ます。 この関数はリストの項を逆順に並び替えます。このような関数の場合、終了条件は空のリストです。 この場合は、なにもひっくり返すことができず、ただ空のリストを返すだけとなります。 他の場合は、自分自身を呼び出すことで duplicate/2 のように終了条件に収束するようにしてみることです。 私たちの関数はリストを [H|T] のパターンマッチを使ってイテレーションしていき、 H を残りのリストの後ろに追加していきます。
reverse([]) -> [];
reverse([H|T]) -> reverse(T)++[H].
長いリストの場合には、このコードは本当の悪夢を見ます。 すべての追加操作がスタックするだけでなく、リスト全体を結合する一つ一つの要素までトラバースする必要があります。 見た目で理解したい人は、このように確認することができます:
reverse([1,2,3,4]) = [4]++[3]++[2]++[1]
↑ ↵
= [4,3]++[2]++[1]
↑ ↑ ↵
= [4,3,2]++[1]
↑ ↑ ↑ ↵
= [4,3,2,1]
ここで末尾再帰の出番です。アキュムレータを使って、毎回それに新しいheadを追加するので、リストは自動的に逆さまになります。 まずは実装を見てみましょう:
tail_reverse(L) -> tail_reverse(L,[]).
tail_reverse([],Acc) -> Acc;
tail_reverse([H|T],Acc) -> tail_reverse(T, [H|Acc]).
これをただの再帰版と同じように展開してみると、こうなります:
tail_reverse([1,2,3,4]) = tail_reverse([2,3,4], [1])
= tail_reverse([3,4], [2,1])
= tail_reverse([4], [3,2,1])
= tail_reverse([], [4,3,2,1])
= [4,3,2,1]
ここからわかることは、リストを逆順に並べるのにアクセスしなければいけない要素の数は線形になったということです。 スタックがどんどん大きくなってしまうことを避けられるだけではなく、ずっと効率的に操作できるのです!
sublist/2 という関数も実装してみましょう。これはリスト L と整数 N を受け取って、リストから最初の N 個の要素のリストを返す、というものです。 例として sublist([1,2,3,4,5,6],3) が [1,2,3] を返すか見てみましょう。 再度確認ですが、終了条件は0個の要素をリストから取得する場合です。しかしながら sublist/2 はちょっと違います。 2つ目の終了条件として空のリストを受け取った場合があります! 空のリストを受け取った場合を確認しないと、 recursion:sublist([1],2) を呼び出したときにエラーが起きます。 ここでは [1] がほしいのです。ここが決まってしまえば、再帰部分はリストをなめるだけとなります。 要素を進むだけ進めて、終了条件にぶつかったらやめます:
sublist(_,0) -> [];
sublist([],_) -> [];
sublist([H|T],N) when N > 0 -> [H|sublist(T,N-1)].
今度は前と同じように末尾再帰に変換してみます:
tail_sublist(L, N) -> tail_sublist(L, N, []).
tail_sublist(_, 0, SubList) -> SubList;
tail_sublist([], _, SubList) -> SubList;
tail_sublist([H|T], N, SubList) ->
tail_sublist(T, N-1, [H|SubList]).
この関数には欠陥があります。致命的な欠陥です! ここではリストを逆順に並べるときと同じようにリストをアキュムレータとして使いました。 もしこの関数をそのままコンパイルすると、 sublist([1,2,3,4,5,6],3) を実行すると [1,2,3] でなく [3,2,1] が返ってきます。 出来ることは、最終結果を自分で逆順にすることです。 tail_sublist/2 をこのように変更して、再帰部分をそのまま残しておきます:
tail_sublist(L, N) -> reverse(tail_sublist(L, N, [])).
これで最終結果は正しい順序になります。 末尾再帰のあとに逆順に並び替えるというのは時間の無駄に思えるかもしれませんし、それは一部で正しいです。 (まださらにメモリを節約することができます) これが原因で短いリストでは、普通の再帰のほうが末尾再帰より末尾再帰版よりも速いと思います。 しかしデータが大きくなるにしたがって、リストを逆順に並び替えるのは楽になります。
Note
reverse/1 を自分で書くよりも、 lists:reverse/1 を使うべきです。 この関数は末尾再帰呼び出しに何度も使われているので、Erlangの保守者と開発者がBIFに追加することに決めました。 リストでは(C言語で書かれた関数のおかげで)とても速いreverse関数を使うことが出来ます。 これによってreverse関数があまり不利にならなくなりました。 この章ではこれ以降も自前のreverse関数を使いますが、それ以降はもう自前のreverse関数は使うべきではありません。
さらに進めて、zip関数を書いてみましょう。zip関数はある長さの2つのリストを受け取って、それぞれのリストの2要素を1つのタプルにまとめて、1つのリストに収めます。 自前で書いた zip/2 関数はこのように動作します:
1> recursive:zip([a,b,c],[1,2,3]).
[{a,1},{b,2},{c,3}]
2つの引数に与えたリストは同じ長さだとして、終了条件は2つの空のリストをzipする状況になります:
zip([],[]) -> [];
zip([X|Xs],[Y|Ys]) -> [{X,Y}|zip(Xs,Ys)].
しかし、zip関数をもうちょっと寛大にするなら、2つのリストの内1つが終わったら終了するようにしたらいいでしょう。 この条件で、2つの終了条件を作ります:
lenient_zip([],_) -> [];
lenient_zip(_,[]) -> [];
lenient_zip([X|Xs],[Y|Ys]) -> [{X,Y}|lenient_zip(Xs,Ys)].
終了条件が変わっても、関数の再帰部分は同じだということに注目してください。 ここで、この zip/2 と lenient_zip/2 を自分で末尾再帰にしてみてください。 それでどのように末尾再帰関数の作り方を完全に理解したとしましょう。 末尾再帰は大きなアプリケーションでループを作る際の大事な概念です。
答えを確認したい場合は、私の実装を recursive.erl で確認してみてください。
Note
ここで見た末尾再帰はメモリ消費量を大きくしません。 なぜなら仮想マシンが関数が自分自身を末尾で呼び出すからです。(関数内で最後の式が評価される) これで現在のスタックフレームを削除します。 これは末尾呼び出し最適化(Tail Call Optimization, TCO)と呼ばれ、終端呼び出し最適化(Last Call Optimization, LCO)と呼ばれる最適化の特殊なケースです。
LCOは関数本体で評価される最後の式が他の関数を呼び出す場合に行われます。 TCOが行われると、Erlang VMはスタックフレームに保存するのを避けます。 末尾再帰は複数の関数の間でも可能です。例として、 a() -> b(), b() -> c(), c() -> a() のような関数の連鎖があるとします。 このときにLCOがスタックオーバーフローを避けてるようにするので、この無限ループはメモリ不足にならず効率的に動作します。 この原則から、アキュムレータを使うことによって末尾再帰が有用なものになるのです。
7.5. 素早く、ソート!¶
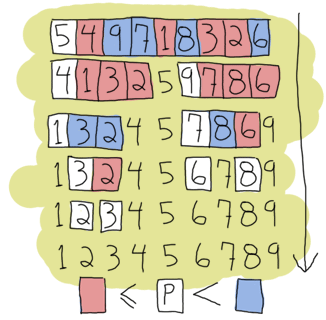
もう再帰と末尾再帰はわかったと思います。でも、確認のためにもっと複雑な例に取り組んでみたいと思います。 クイックソートです。そうです、あの伝統的な「おい、見ろよ、俺なんて短い関数型的なコードが書けちゃうんだぜ」という自慢ととして権威のある例です。 クイックソートの自然な実装は、最初のリストの要素をピボットとして、それ以下の要素とそれより大きい要素をそれぞれ別の新しいリストに入れます。 それからそれぞれのリストで同じことを繰り返していって、どんどんソートするリストが小さくなって、最後にはソートするリストが空になります。これが終了条件です。 この実装が自然と言われるのは、より速いクイックソートは速くなるように最適なピボットを選ぼうとするからです。 ですが、今回は例なのでそこまで気にしません。
2つの関数が必要です。1つ目はリストを小さいものと大きいものに分ける関数で、2つ目は新しいリストに1つ目の関数をそれぞれ適用させてからくっつける関数です。 まず最初に、くっつける関数から書きましょう:
quicksort([]) -> [];
quicksort([Pivot|Rest]) ->
{Smaller, Larger} = partition(Pivot,Rest,[],[]),
quicksort(Smaller) ++ [Pivot] ++ quicksort(Larger).
このコードでは、まず終了条件があって、次にすでに大きい分部分と小さい部分に他の関数によって分けられたリスト、ピボットを使ってその前後にクイックソートされたリストをくっつけるということをしています。 これがリストをまとめる役割をしているわけです。今度は小さいものと大きいものに分ける関数です:
partition(_,[], Smaller, Larger) -> {Smaller, Larger};
partition(Pivot, [H|T], Smaller, Larger) ->
if H =< Pivot -> partition(Pivot, T, [H|Smaller], Larger);
H > Pivot -> partition(Pivot, T, Smaller, [H|Larger])
end.
これでクイックソート関数を実行できます。以前にErlangでの例をインターネットで見たことがあれば、他のクイックソートの実装を見たことがあるかもしれません。それはもしかするともっと簡素で読みやすいもので、リスト内包を使っていたかもしれません。 リスト内包で置き換えやすい部分は新しいリストを partition/4 関数で作成するところです:
lc_quicksort([]) -> [];
lc_quicksort([Pivot|Rest]) ->
lc_quicksort([Smaller || Smaller <- Rest, Smaller =< Pivot])
++ [Pivot] ++
lc_quicksort([Larger || Larger <- Rest, Larger > Pivot]).
ずっと読みやすくなった代わりに、リストを2つに分けるために一旦リストを走査してやらなければいけません。 これは読みやすさとパフォーマンスとの勝負ですが、負けはあなたです。 なぜなら lists:sort/1 という関数がすでにあるからです。代わりにそれを使ってください。
Don’t drink too much Kool-Aid
このような簡潔なコードはお勉強としてはいいですが、パフォーマンスはよく有りません。 多くの関数型プログラミングのチュートリアルではこの点に触れていません! なによりもまず、いま取り組んだどちらの実装も一度以上ピボットと等しい値を処理擦る必要があります。 パフォーマンスを上げるために、ピボットより小さい、大きい、等しいの3つのリストを返すこともできたはずです。
別の問題として分けられた関数をピボットにくっつけるときに、どうしてそれらを一度以上走査する必要があるのかということです。 リストを3つに分けるときにリストの結合をすることでオーバーヘッドをちょっと抑えることが出来ます。 こういったことに興味があるなら、 recursive.erl の最後の関数(bestest_qsort/1)を参考にしてみてください。
これらのクイックソートでのいい点はどんなデータ型のリストにも動作することです。 たとえタプルのリストだろうがなんだろうがです。試してください。動きます!
7.6. リストを超えて¶
この章を読んで、Erlangでの再帰というのはリストでなにかをすることだと思い始めたでしょう。 リストは再帰的に定義できるデータ構造のいい例ですが、リスト以外にもそういうものはあります。 多くの例をみるために、二分木を作ってそこからデータを読み込んで見ましょう。

まず最初に、木とは何かを定義することが重要です。私たちの例では、端から端までノードです。 ノードはキーと値、そして他の2つのノードを持ったタプルにで表現されます。 タプルの中にある2つのノードはそれぞれ保持してているキーよりも小さい値のキーと大きい値のキーを持つノードが必要です。 そうです、これは再帰です!木はノードがノードを持っていて、そのノードがまたノードを持っていて、またそれらがノードを持っていて、という具合です。 これは無限に繰り返すことはできないので(無限データを保存するわけではないので)、ノードは空のノードも持つことができます。
ノードを表すのに、タプルは適切なデータ構造です。私たちの実装では、このタプルを {node, {Key, Value, Smaller, Larger}} と定義します。(タグ付きタプルです!) このときSmallerとLargerは別の同様のノードか空のノードになります。( {node, nil} ) これより複雑なものは必要ありません。
さあ、とても基本的な 二分木モジュールの実装 を始めましょう。 最初の関数の empty/0 を実装しましょう。これは空のノードを返します。 空のノードは二分木を作る上で起点となります:
-module(tree).
-export([empty/0, insert/3, lookup/2]).
empty() -> {node, 'nil'}.
この関数を使うことで、同様にして二分木の実装を隠すことですべてのノードをカプセル化して、人々にその作り方を意識させないようにできます。モジュールにそういう情報を押し込めます。 ノードの表現方法を変えたい場合は、外部コードを変更せずに変えることが出来ます。
二分木にノードを追加するには、まずどのように再帰的にたどるかを理解しなければいけません。 他の再帰の例と同様に終了条件を見つけることからはじめてましょう。 空の木は空のノードです。したがって、終了条件は空のノードです。 空のノードに突き当たったときは、そこに新しいキー/値を追加することが出来ます。 その他の場合はノードを追加できる空のノードを探して木を辿ります。
ルートから空のノードを探すには、 小さい ノードと 大きい ノードがあることによって、挿入するノードの新しいキーと比較ができ、たどることが出来ます。 新しいキーがいまいるノードのキーより小さければ、小さいほうのノード内を探せばよく、大きければ大きい方のノードを探せばいいのです。 しかしもう1つの状況があります。もし新しいキーがいまのノードのキーと同じだったらどうしましょう? 2つの選択ができます。プログラムを失敗とさせるか、値を新しい値に書き換えるかです。 これはオプションです。このロジックが動作するように関数を次のように実装します:
insert(Key, Val, {node, 'nil'}) ->
{node, {Key, Val, {node, 'nil'}, {node, 'nil'}}};
insert(NewKey, NewVal, {node, {Key, Val, Smaller, Larger}}) when NewKey < Key ->
{node, {Key, Val, insert(NewKey, NewVal, Smaller), Larger}};
insert(NewKey, NewVal, {node, {Key, Val, Smaller, Larger}}) when NewKey > Key ->
{node, {Key, Val, Smaller, insert(NewKey, NewVal, Larger)}};
insert(Key, Val, {node, {Key, _, Smaller, Larger}}) ->
{node, {Key, Val, Smaller, Larger}}.
関数が全く新しい木を返すことに注意してください。 これは関数型言語が束縛を一つしか持てないという典型例です。 これは効率的でないように見えますが、変更前後の二分木ではほとんど構造が一緒で、したがって共有されて、仮想マシンによって必要なときだけコピーされます。
この二分木の例で、あとしなければいけないことは lookup/2 関数です。 これはキーを与えることで木から値を探すというものです。 ロジックは二分木に新しいノードを探すときに使ったものとほぼ一緒です。 探しているキーが今いるノードのキーと等しいか、小さいか、大きいかという具合です。 2つの終了条件があります。1つはノードが空の場合(キーが二分木の中になかった場合)でもう1つはキーが見つかった場合です。 キーが見つからなかった場合にプログラムをクラッシュさせたくないので、見つからなかったときには’undefined’というアトムを返します。 そうでなくて見つかった場合は {ok, Value} を返します。 こうする理由は、もし値だけ返すとノードが’undefined’というアトムを持っていた場合、二分木が正しい値をもっていたのかそれとも検索に失敗したのか違いがわからないからです。 このようなタプルで成功したことをラップしておくと、今言ったような混乱がありません。 次に関数の実装を示します:
lookup(_, {node, 'nil'}) ->
undefined;
lookup(Key, {node, {Key, Val, _, _}}) ->
{ok, Val};
lookup(Key, {node, {NodeKey, _, Smaller, _}}) when Key < NodeKey ->
lookup(Key, Smaller);
lookup(Key, {node, {_, _, _, Larger}}) ->
lookup(Key, Larger).
これで終わりました。小さいEmailアドレス帳をつくることでテストしてみましょう。ファイルをコンパイルしてシェルを起動します:
1> T1 = tree:insert("Jim Woodland", "jim.woodland@gmail.com", tree:empty()).
{node,{"Jim Woodland","jim.woodland@gmail.com",
{node,nil},
{node,nil}}}
2> T2 = tree:insert("Mark Anderson", "i.am.a@hotmail.com", T1).
{node,{"Jim Woodland","jim.woodland@gmail.com",
{node,nil},
{node,{"Mark Anderson","i.am.a@hotmail.com",
{node,nil},
{node,nil}}}}}
3> Addresses = tree:insert("Anita Bath", "abath@someuni.edu", tree:insert("Kevin Robert", "myfairy@yahoo.com", tree:insert("Wilson Longbrow", "longwil@gmail.com", T2))).
{node,{"Jim Woodland","jim.woodland@gmail.com",
{node,{"Anita Bath","abath@someuni.edu",
{node,nil},
{node,nil}}},
{node,{"Mark Anderson","i.am.a@hotmail.com",
{node,{"Kevin Robert","myfairy@yahoo.com",
{node,nil},
{node,nil}}},
{node,{"Wilson Longbrow","longwil@gmail.com",
{node,nil},
{node,nil}}}}}}}
そしてEmailアドレスを探してみます:
4> tree:lookup("Anita Bath", Addresses).
{ok, "abath@someuni.edu"}
5> tree:lookup("Jacques Requin", Addresses).
undefined
リストでない再帰のデータ構造による関数型のアドレス帳の例が無事終わりました! では早速Anita Bathさんにメールを...
Note
いま書いた二分木の実装にはまだ必要最低限の機能しかありません。 ノードを削除したり、検索を速くするための二分木の再構築などといったよくある操作がサポートされていません。 もしこういったことに興味があるようでしたら、Erlangの gb_tree モジュール(otp_src_R<version>B<revision>/lib/stdlib/src/gb_trees.erl)を勉強してみるのがいいかもしれません。 木構造を扱うときは自分で車輪の再発明をするよりは、このモジュールを使ったほうがいいと思います。
7.7. 再帰的に考える¶
この章に書いてあったことをすべて理解したのなら、再帰的に考えるということがおそらくより直感的になっていると思います。 再帰的な定義というのを手続き型言語でのそれ(whileやforループ)と比較した場合、その違いは手順を追ったアプローチ(「これをしたら次にこれをして、その後これをして、それでおしまい」)というよりはより宣言的なもの(「こういう入力を得たら、こうして、そうでなければこうする」)だということです。 この特性は関数の先頭でパターンマッチをしているときにより明確になります。
もしまだ再帰がどのように動作するか理解してなければ、次の文章を読むと分かるようになるかもしれません。
冗談はさておき、パターンマッチを使った再帰は理解しやすい簡潔なアルゴリズムを書くときには最適解であるときがあります。 問題を細かい部分に分割して、それをこれ以上簡単にできない程まで別々の関数に分けてやれば、アルゴリズムの実装は小さいルーチンから得られる正しい答えの寄せ集めに過ぎなくなります。(クイックソートでやったことと似ていますね) こういった精神的な抽象化は日常生活の繰り返しにおいても可能ですが、その練習は再帰で簡単にできます。 あなたのこれからが変わるでしょう。
紳士淑女の皆様、議論です:著者と彼自身の議論です
- よし、これで再帰は理解したぞ。宣言的だということがわかった。 数学的な面があって変数は変えられないというのもわかった。 場合によっては簡単に書けるということも分かってもらえたはずだ。で、他に?
- 決まったやり方があるんだ。終了条件を探して書きだす。 その後他のケースを結果が出るように終了条件に絞り込んでいく。 これで関数を書くのがとても簡単になるぞ。
- よし、わかった。もう何度もやったんだね。ループも同じことをするよ。
- そうだね、それは間違いない。
- だよね。で、わからないのは、もし末尾再帰よりパフォーマンスが悪いなら、なんで末尾再帰じゃない普通の再帰関数をいちいち書くなんていう紛らわしいことをしていたのかってこと。
- あ、それは理解しやすくするためさ。見やすくて理解しやすい普通の再帰から、理論的により効率のいい末尾再帰に移行するのはやり方を全部見せるのにいい方法だと思ったんだ。
- なるほど、じゃあ普通の再帰はお勉強の時以外は役に立たないってことだね。了解。
- それがそうでもないんだ。実際には末尾再帰と普通の再帰ではほとんどパフォーマンスの差を見ることはないと思うよ。 気をつけなければいけないのは、メインループのように無限ループをするときや大きなデータセットを操作するときなんだよ。 末尾再帰にしないと、とても大きなスタックをいつも作って、遅くなって、すぐクラッシュしてしまう関数があるんだよ。 こういう関数のいい例はフィボナッチ関数だよ。この関数は逐次的か末尾再帰にしないと指数関数的に大きくなってしまうんだ。 コードのプロファイルを取って(あとでどうやってプロファイルをとるか見せるよ、約束する)、何が遅くしてるか見て、直そう。
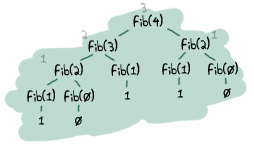
- でもループをいつも逐次的に書けばこんな問題は起きないよ
- うん、でも...でも...僕の美しいErlangが...
- でもそれじゃあすごくなくない?だってこういうことを覚えなきゃいけないのはErlangに’while’とか’for’がないからじゃん。 どうもありがとう、もうC言語でプログラミングすることにするよ!
- ちょっと待った!関数型プログラミング言語にはほかにもいい点があるよ! 終了条件を見つければ再帰関数を書くのがずっと簡単になるよ。 たくさんのかしこい人が再帰関数自体をあんまり書かなくていい方法も見つけてくれたよ。 もしそこで待っててくれれば、どうやってそういうやり方ができるかを見せるよ。 でもそれにはもっと力をつけないといけないんだ。高階関数について説明させてくれ...
